Pi sayısının yanında daha gizemli görünen e sayısı adını ünlü matematik Euler’in baş harfinden alır. Bir diğer ismi de Euler sabitidir.
Yaklaşık değeri;
Peki Bernoulli Bu Sayıyı Nasıl Buldu?
Problemden bahsedecek olursak;
Örneğin 100 TL paramız olduğunu düşünelim. Bir banka yıllık %5 bileşik faizde bankaya yatıracak olursak bir yılda paramız 105 TL olur. İkinci yılda 105*1,05 olur. Her yıl yeni fiyattan faiz işler ve para gittikçe büyür.
Şimdi de 1 TL paramız olduğunu düşünelim;
►Yılda %100 faiz veren bir bankaya yatırırsa 1 sene sonra 2 lirası olur.
► 6 ayda bir %50 faiz veren bir bankaya yatırırsa 1 sene sonra 2,25 lirası olur.
► 3 ayda bir %25 faiz veren bir bankaya yatırırsa 1 sene sonra 2,44… lirası olur.
► Ayda bir %8,33… faiz veren bir bankaya yatırırsa 1 sene sonra 2,6130… lirası olur.
► Ve aynı şekilde haftada bir işleyen faiz sonunda 1 sene sonra 2,6925… lirası olur.
► Her gün işleyen faizi hesapladığımızda ise 1 sene sonra 2,71453… lirası olur.
Bunu formülize edecek olursak;
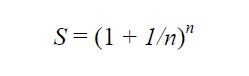


Faiz süresini kısalttığımızda e sayısına daha da yaklaşmış oluruz.
n sayısının sonsuzda limitini aldığımızda e sayısı bu şekilde ifade edilir;
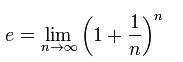
Ayrıca e sayısı şapka probleminde de karşımıza çıkar. Şapka problemi şudur:
Bir restorana giren ve girişte şapkalarını vestiyere bırakan n tane müşteri düşünelim. Vestiyer, şapkalara etiket takmayı unutunca hangi şapkanın hangi müşteriye ait olduğunu unutuyor, ve çıkışta şapkasını isteyen her müşteriye rastgele bir şapka seçip veriyor. Bu durumda, n müşteriden hiçbirinin kendi şapkasını almaması olasılığı nedir?
Problemin çözümünde hiç kimsenin kendi şapka almama olasılığı:
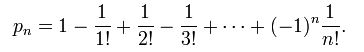
► e sayısı aşağıdaki toplama eşittir.

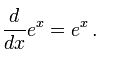
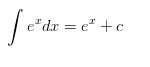
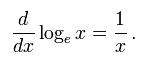
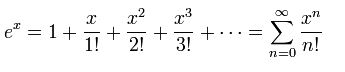
Bu saydıklarımızın dışında gizemli e sayısının ve fonksiyonlarının bir çok özelliği vardır.
Euler e sayısını, virgülden sonra 23. basamağına kadar hesaplayabilmiştir. Günümüzde ise e sayısının milyarlarca basamağı bilinmektedir. e’nin irrasyonel bir sayı olduğu Euler tarafından kanıtlanmıştır.
Matematik dünyasında belki biraz π’nin gerisinde kalmış gibi görünse de e sayısı aslında en az π sayısı kadar değerli bir sayıdır. Bileşik faizde yer alan formülün limit değerinde n artarken kesin değeri 2.71828 fark edildiğinde ortaya çıkmıştır. Daha sonra ise ex olarak tanımlanacak olan ve türevinin yine kendisine eşit olduğu, logaritmik fonksiyonun tersinin ortaya çıkmasıyla matematikte daha popüler olmuştur.
Kaynak:
bilimsehri.com
wikipedia.org
mathworld.wolfram.com
 Mehmet Ali Mersin
Mehmet Ali Mersin
