Üniversite yıllarımda matematikte ilginç ifadeler ararken bulmuştum Möbius Şeridini. Bilindiği üzere üç boyutlu bir cisim olmasına rağmen tek bir yüzeye sahiptir bu şerit. Yani bir kalemi kaldırmadan her tarafını gezebilir, bir karınca yürümeye başladığında yönünü değiştirmeden sadece düz yürüyerek her tarafını gezebilir.

İlk defa 1861’de Johann Benedict Listing tarafından tanımlanan bu şerit .August Ferdinand Möbius, bir çalışmasında tanımını vermiş ve şeridin tek yüzlü olmasını, yönlendirilememesiyle açıklamıştır.
Möbius şeridini elde edebilmek için cetvel şeklindeki kağıt bir şeridin bir ucunu 180 derece büküp diğer ucu ile birleştirmek yeterlidir.
Bu şeridi aslında sıkça gördüğümüzü de söyleyebilirim. Recycle yani geri dönüşüm işareti buradan gelmiştir.
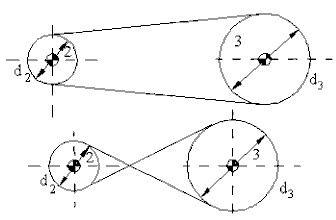
Ayrıca mekanik alanındaki faydasını unutmayacak olursak; motor kayışının takılma şekli örnek verilebilir. Yani düz şekilde bağlanırsa bir yüzeyi kullanılacağından hemen yıpranır. Ama Möbius Şeridindeki gibi bağlanırsa her iki yüzey eşit oranda yıpranır ve daha uzun süre dayanır.
Moebious Şeridi’nin parametrik denklemi:
f(u, v) = ( (cos(u) + v*cos(u/2)*cos(u)), (sin(u) +v*cos(u/2)*sin(u)), v*sin(u/2)), 0 <= u <= 2*pi, -0.3 <= v <= 0.3
Son olarak M.C. Escher‘in bu konu ile ilgi yaptığı çalışmaları da araştırmanızı tavsiye ederim.
 Mehmet Ali Mersin
Mehmet Ali Mersin

Teşekkür ederim yazdıklarınız için, internette bu konu hakkında bu kadar geniş ve yeni kapılar açan bir yazı bulamamıştık.